Title : System Oscillation

|
Location : Home > Methods > Simulation > System Dynamics > Introduction to System Dynamics Title : System Oscillation |
 |
System Oscillation
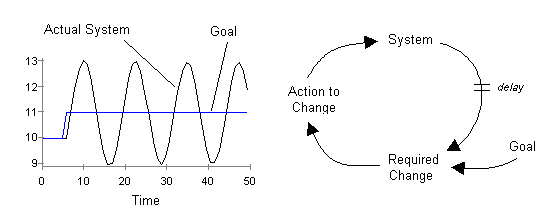
Figure 1: System oscillation is created when decision information in negative feedback structures is delayed.
Figure 2 shows a simple system in which the information about the current "level" of the system variable first passes through a single stock/flow structure before being used to take a controlling action (information path is shown in red). Thus, the decision to take action by changing the variable, Action, is based not on the current state of the system but on some previous value.
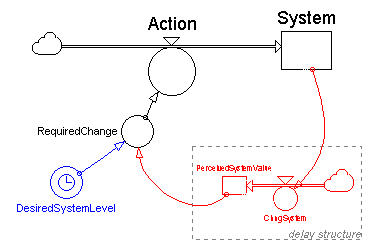
Figure 2: Simple negative feedback structure with control information delay.
Given this structure, Figure 3 shows what happens if the goal, DesiredSystemLevel, is increased by 5 units. Because of the delay, the system overshoots its target at about time=6, reaches a maximum of 22 units at time=10, then undershoots at about time=12, and so on. Eventually, the system does find its target 50 time units after the goal changed!
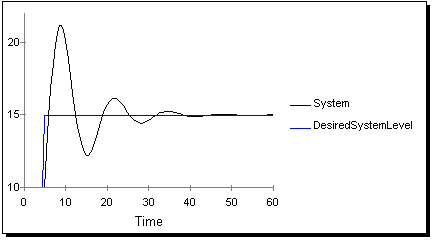
Figure 3: A step increase in goal value causes a damped oscillation response in system.
Elephant-Hunter Model Example
Figure 4 presents a more complex example of a system that exhibits oscillatory behavior. In this Elephant-Hunter Model, the conservation and health of the elephant herd is directly dependent on the ability of the park manager to keep the herd population below the carrying capacity of the land. Too many elephants will result in long-term damage to the park's feed production capacity and ultimately reduce the number of elephants that can be sustained. (click on image to run simulation)
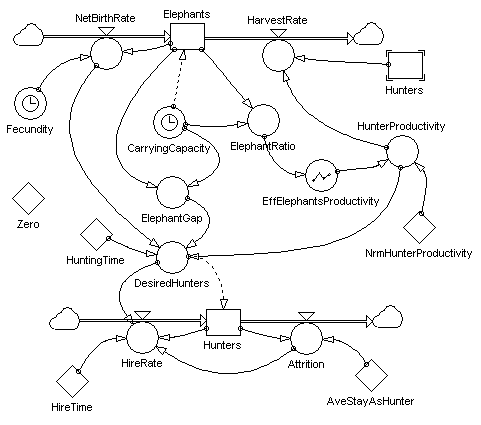
Figure 4: Elephant-Hunter system structure.
One of the primary herd control "leverage points" in this system is to change the rate at which elephants are "harvested" by increasing or decreasing the number of hunters. Keep in mind that the elephant population level is a function of the elephant Net Birth Rate and the Harvest Rate. Thus, by increasing the hiring rate of hunters, the total number of hunters will increase. An increase in the number of hunters will increase the elephant harvest rate. An increase in harvest rate will "draw down" the level of elephants in the herd.
Consider a scenario in which the net birth rate of the elephant herd increases from 8 elephants per year to 12 elephants per year. Due to inherent delays in herd data gathering and analysis methods, this increase is not immediately detected. After some delay, the birth rate trends are revealed and the manager decides to hire more hunters. However, because of the delays in hiring, more time passes before the hunters are actually onboard. As the hunter population increases, the harvest rate increases, which causes the herd population growth to slow, stop, and eventually turn downward. Since the system delays are still in place, however, the herd level continues to drop and eventually undershoots the target, prompting the manager to reduce the number of hunters. This "trial and error "oscillating process continues until the equilibrium target is reached, almost 20 time units from the initial step increase in birth rate! Figure 5 and 6 shows the results of this scenario.
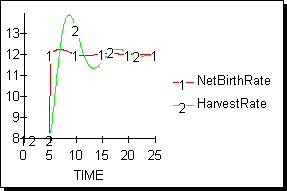
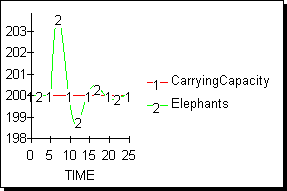
Figure 4: Results of a step increase in elephant birth rate.
Types of Oscillations
Information delays are prevalent in the real world so it's no surprise that oscillations are the most common dynamic behaviors. There are four basic types:
| Sustained Oscillation |
|
| Damped Oscillation |
|
| Exploded Oscillation |
|
| Chaos Oscillation |
|
[Previous] |
[Next] |
 |
Update : 2005/07/23 |