Title : Implications of System Structure

|
Location : Home > Methods > Simulation > System Dynamics > Introduction to System Dynamics Title : Implications of System Structure |
 |
Implications of System Structure
One of the reasons that mental models are so complex is simply that the real-world systems that humans are trying to understand are highly complex. Over the years, system dynamicists have identified characteristics that seem to appear again and again in real-world systems -- particularly social systems. They have found that: (1) symptoms of a problem are often separated from the actual problem by time and space; (2) complex systems often behave counter to human intuition; (3) policy intervention in complex systems can frequently yield short-term successes but long-term failure, or the reverse; (4) internal system feedback often counters external policy intervention;(5) it is better to structure a system to withstand uncertain external shocks than to try to predict those external shocks; (6) real-world complex systems are not in equilibrium and are continually changing. These characteristics arise due to the nonlinear stock, flow, feedback structures of social systems.
A System Problem and Its Symptoms are Separated By Time and Space
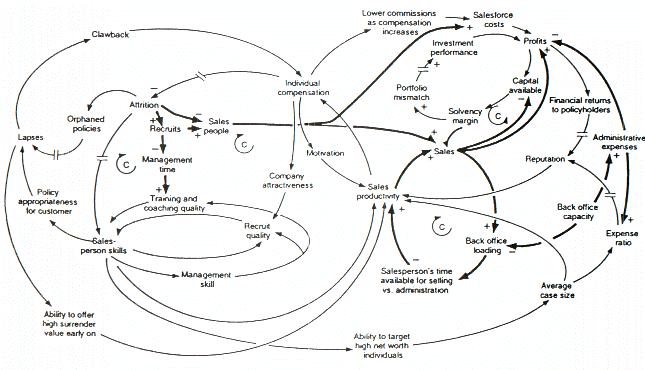
| Beyond Ghor was a city. All its inhabitants were blind. A king with his entourage arrived nearby; he brought his army and camped in the desert. He had a mighty elephant, which he used in attack and to increase the people's awe. The populace became anxious to learn about the elephant, and some sightless from among this community ran like fools to find it. Since they did not know even the form or shape of the elephant, they groped sightlessly, gathering information by touching some part of it. Each thought that he knew something because he could feel a part. When they returned to their fellow-citizens, eager groups clustered around them, anxious, misguidedly, to learn the truth from those who were themselves astray. They were asked about the form, the shape, of the elephant, and they listened to all they were told. The man whose hand had reached the ear said, "It is a large, rough thing, wide and broad, like a rug." One who had felt the trunk said, "I have the real facts about it. It is like a straight and hollow pipe, awful and destructive."One who had felt its feet and legs said, "It is mighty and firm, like a pillar." Each had felt one part out of many. Each had perceived it wrongly. Idries Shah. 1969. "The Blind Ones and the Matter of the Elephant," p. 25. In: Tales of the Dervishes. New York: E. P. Dutton. |
Counterintuitive Behavior
Nonlinear stock-flow-feedback systems frequently behave in ways that are counterintuitive or different from that which a decision maker's unaided mental model would suggest -- particularly in response to the dynamics of a policy change. Forrester notes, for example, that both the places where "high leverage points" (i.e., places at which a policy change can permanently alter a system's behavior) are located, and the direction in which a decision maker must "push" a system to change it's behavior, are counterintuitive. Frequently, the counterintuitive behavior of social systems is due to the existence of negative feedback loops. As an example, consider a small sailboat with a rudder in the stern. If the sailor operating the boat wishes to turn the bow (front) to the starboard (right), he or she must turn the rudder, located in the stern, to port (left). In other words, he or she must intervene with a policy change (turn the rudder) in a place (the stern) different from where the change will manifest itself (the bow) and in a direction (port) opposite from the one desired for the entire system (starboard). A sailboat is a negative feedback system in the sense that there is a desired direction the sailor wishes to point the bow of the boat and an actual direction the bow of the boat is pointing. If a discrepancy develops between the desired direction and the actual direction, corrective action (moving the rudder) is taken. A second example of a simple negative feedback loop system that can exhibit counterintuitive behavior is a thermostat. Consider the following thought experiment. If a person is given a cigarette lighter (i.e., a small heat source) and an ice cube (i.e., a small source of cold) and asked to apply one to the sensor on the thermostat to make a room warmer, which one should he or she choose? The answer, of course, is the ice cube because applying a cold source to the thermostat's sensor would cause the furnace to turn on and heat the room.
Better Before Worse or Worse Before Bettery
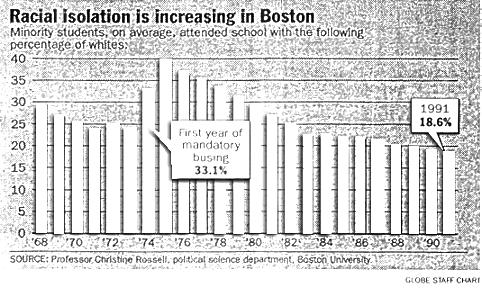
Policy Resistance
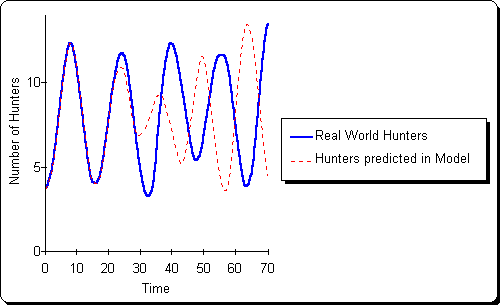
Unpredictability

Disequilibrium
As was pointed out earlier, all actual social systems exist in a state of disequilibrium. This implies that actual social systems possess on-going pressures for change, and stocks that decouple flows and allow inflows to differ from outflows. It also implies that using equilibrium-based modeling techniques, such as many of those used in economics and management, will frequently not yield insights that directly relate to the dynamic behavior of actual social systems.
[Previous] |
[Next] |
 |
Updated : 2006/02/07 |