Location : Home > Methods > Simulation > System Dynamics > Introduction to System Dynamics Title : Taking A Dynamic Perspective

Taking A Dynamic Perspective

　システムダイナミクスは時間とともに変化するシステムの振る舞いに関心がある。システムや問題を検証するにおいて重要な段階は主要な振る舞いのパターン−「時間経路（Time Paths）」として参照する−を特定することである。このセクションでは、時間経路の意味を確認し、動的なシステムに共通して見られる一般的なタイプを検討する。この議論に関する現実的な基礎を示すために、書籍や新聞、雑誌などに現れたいくつかの時間系列の例を以下に挙げる。

Time Paths

　システムダイナミクスモデリングはシステムの動的な振る舞いに関心がある。すなわち時間とともに変化するシステムの振る舞いである。システムダイナミクスモデリングでは、モデル作成者は重要なシステム変数で示される振る舞いのパターンを特定しようと試み、パターンを踏襲できるモデルを構築する。いったんモデルがこの能力を持てば、望むようにシステムの振る舞いを変更することを狙った政策を検証するための実験室として活用することができる。
　図１は正の傾きを持つ直線であるが、これは動的時間経路の例でもある。現実のシステムはさまざまな時間経路を（しばしば同時に）示すが、いいことに、明らかに区別できる時間経路の「族（"families"）」は比較的少ない。

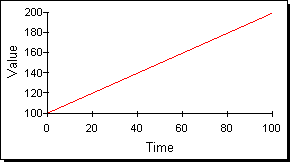
図１：時間経路の例

　図２から５までは現実の世界でよく起こる15の異なる時間経路を示す。これらの経路は５つの族に分類され、それぞれを以下に記す。このほかにももっと複雑なパスは見受けられるが、たいていはここに示す経路の組み合わせであることが多い。

Linear Family

　最初の族は図２に示すような線型族である。線型族には均衡状態（equilibrium）・線型成長（linear growth）・線型下降（linear decline）が含まれる。これらの時間経路は単純でかつ直感的であるので、システムダイナミクスモデリングに関して独自のものの見方で置き換えていること性を指摘することは重要である。

図２：線型族の時間経路

　注意すべき最初の点は、平均的な人−システムモデリングの訓練を受けていない人−が現実のシステムも（図２の２番目や３番目の示されるような）線型に増加または減少していると思ってしまいがちだということである。しかしながら実際にはほとんどのシステムは線型に増加または減少などしないし、むしろ（図３に示すような）指数的な振る舞いに従う。純粋な線型時間系列はたいていフィードバック−現実のシステムにおいてもシステムダイナミクスモデリングにおいてもきわめて重要な構成ブロックである−のないシステムである。
　注意すべき第２の点は、図２に示す均衡時間経路は現実のシステムではほとんど見られない振る舞いだということである。もはや変化への圧力がまったくない完全な均衡状態のことである。実際には、システムダイナミクスの観点からは均衡状態とは、システムの全ての状態変数が同時に望むべき値に達すること−きわめて人為的な状態−を指す。奇妙なことだが、現代の経済・経営科学で用いられているモデルの多くが均衡の概念に基づいている。一方、システムダイナミクスでは最も興味深いシステムの振る舞い（問題）は非均衡なものであり、最も効果的なシステムダイナミクスモデルは非均衡名時間経路を示すと信じられている。しかしこのことは均衡が無用だということを意味するわけではない。反対に、政策による「純粋な」影響を研究するためにシステムダイナミクスモデルで均衡状態を初期条件に設定する場合もある。

Exponential Family

　２つめの時間系列の族は図３に示されるような指数族である。指数族には指数的成長と指数的減衰がある。前述したように現実のシステムは線型の時間経路をとるのではなく指数時間系列に従う傾向がある。

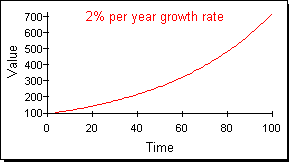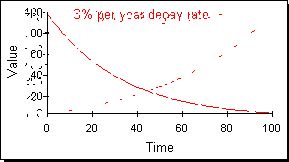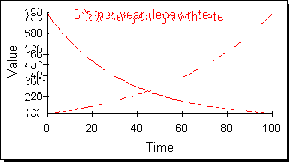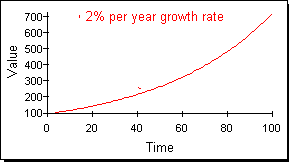
図３：指数族の時間経路

Goal-seeking Family

　３つめの時間系列の族は図４に示されるような目標探索（goal-seeking）族である。あらゆる生物システムは（多くの非生物システムもだが）目標探索的な振る舞いを示す。目標探索的振る舞いは指数的減衰に関連がある。図３の２番目の時間系列と図４の２番めの時間系列を比較するとよい。この２つの唯一の違いは、図３では０に向かって小さくなっていくが、図４では０でない値に向かっている。

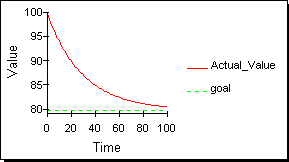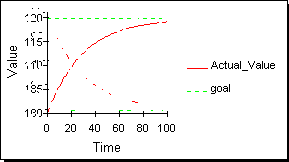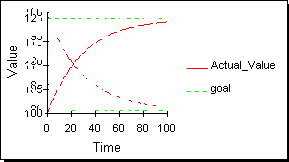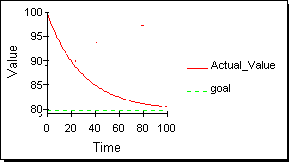
図４：目標探索族の時間経路

Oscillation Family

　４つめの時間系列の族は振動（Oscillation）族である。振動は世界で最もよく見られる動的振る舞いの１つであり、様々なパターンで特徴付けられる。図５では持続（sustained）・減衰（damped）・発散（exploding）・カオス（chaos）の４つのパターンを示しておいた。

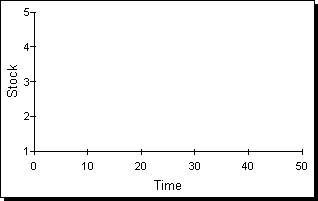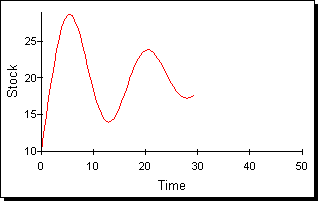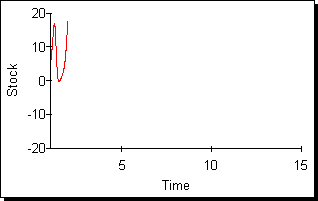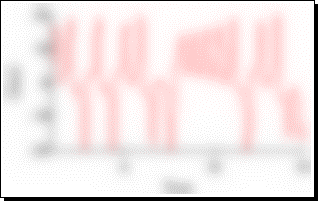
図５：振動族の時間経路

　持続性のある振動には周期（サイクルが繰り返されるまでのピークの数）がある。持続的振動はその周期で特徴付けることができる。減衰振動は損失や緩和のプロセスを示すシステムで現れる。損失や緩和プロセスの例としては、物理システムにおける摩擦や社会システムにおける情報平滑化が挙げられる。発散振動は持続的振動パターンに落ち着くかまたはシステムが分割されるまで成長し続ける。結果として現実の世界では発散振動はさほど頻繁には現れないし、さほど長い間持続しない。カオス的振動は振動はしているのだが不規則に変動し、決して繰り返しがない（すなわち周期は本質的に無限大）。カオスは、ランダム性がないシステムから本質的にランダムなパターンが生成されるため、時間系列の独特な型である。

S-shaped Family

　５つめの時間系列の族は図６に示されるようなＳ型（S-shaped）族である。Ｓ型の成長時間系列を詳細に見れば、指数成長型と目標探索型の２つの時間系列の組み合わせであることがわかるであろう。簡単に言えば、Ｓ型成長の場合はシステムが限界や収容能力（緑色の線で示されている）に近づくと指数的成長が目標探索型に変わると理解すればよい。

図６：Ｓ型族の時間系列

　しかしながら、時にはシステムが収容限界を超える（overshoot）場合がある。オーバーシュートが起こった場合、システムの収容限界が破壊されるのではなく、その限界の周辺を振動することが多い。反対に、オーバーシュートした際に収容限界がダメージを受けた際にはシステムは最終的に崩壊する。これは「オーバーシュート＆崩壊（"overshoot and collapse"）システム応答と呼ばれる。オーバーシュートに対する応答の第３の可能性はシステムが単純に反対に向かい、逆Ｓ型パターンにしたがってシステム容量に近づくという振る舞いである。通常のＳ型と同様、逆Ｓ型は指数的減衰と下降の自己強化スパイラルの組み合わせである。

---

Actual Data

　 Jay Forrester はシステムダイナミクスの授業で生徒に「新聞を様々な観点で読んで学びなさい」と言っていた話はよく引き合いに出される。システムダイナミクスを学んだ後では、メディアに現れる実際のグラフや時間系列を違った観点で見ることができるだろう。
　図１から１０では、ここ数年の様々な書籍や新聞、雑誌から選んだ実際の時間経路のグラフを示している。それぞれの図表を説明すれば、前セクションでの時間系列のどれにあたるかを特定できるだろう。

　例えば図１は実際の1967年から1994年までの高齢者向け医療保険制度（Medicare）の費用のグラフである。このグラフから２つのことが言える。１点目は高齢者向け医療保険制度の費用は1967年から1994年までは線型に増加すると予測されていた−システムのダイナミック性に通じていない人がよく犯す過ちだが−ことである。２点目は現実の高齢者向け医療保険制度の費用は1967年から1994年まで指数的に増加したということである。

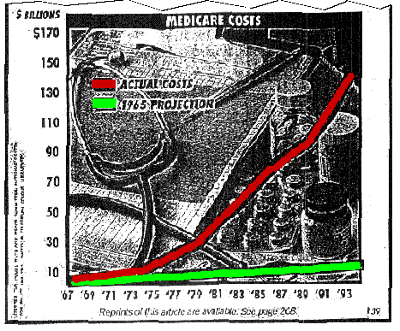
図１：高齢者向け医療保険制度の費用の予測と実態（1967 - 1994）

　図２は1960年から1993年の間に報告された合衆国における麻疹（はしか）の患者数のグラフである。この形状は明らかに指数的減衰を示している。

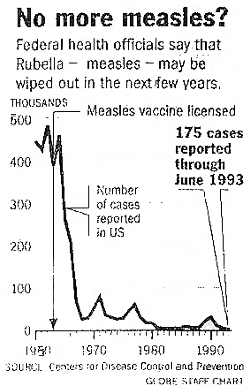
図２：麻疹の患者数の推移（1960 - 1993）

　図３は1988年から1993年までの NBA の観客動員数のグラフであり、図４は合衆国における 486 デスクトップコンピュータの平均販売価格のグラフである。これらのデータは非零の目標探索時間経路を示している。

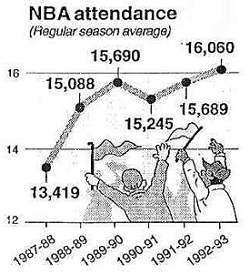
図３：NBA 観客動員数の推移（1988 - 1993）


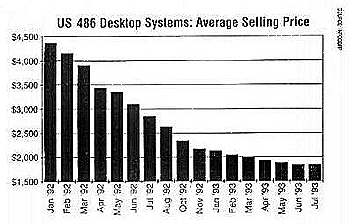
図４：合衆国における 486 デスクトップコンピュータの平均販売価格の推移

　図５は1821年から1933年までのカナダにおける大山猫捕獲数のグラフ（対数表示）である。若干ノイズが乗り、不規則ではあるけれども、持続的振動に分類できるであろう。

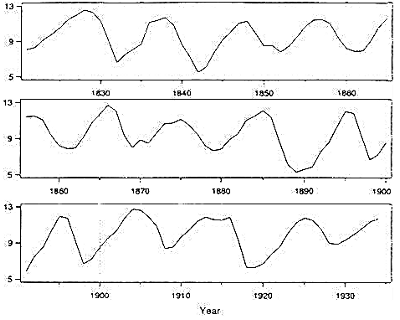
図５：カナダにおける大山猫捕獲数の推移（対数表示；1821 - 1933）

　図６は1957年から1978年までのノルウェーのパルプの在庫・生産・販売のグラフである。パルプの在庫量は発散振動を示している。

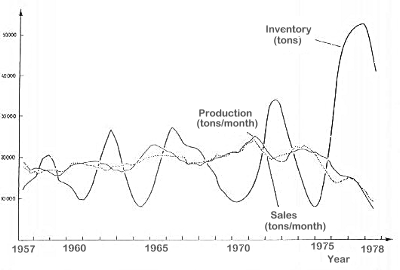
図６：ノルウェーにおけるパルプの在庫・生産・販売量の推移（1957 - 1978）

　図７は合衆国郵政公社で1981年から1991年までに取り扱った第3種郵便物のグラフ（単位は10億通）である。これはＳ型を示している。

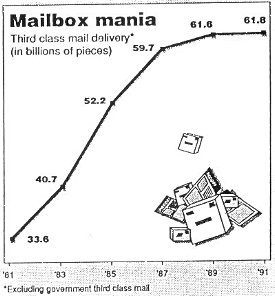
図７：合衆国郵政公社における第3種郵便物取扱量（単位10億通；1981 - 1991）

　図８は合衆国における1900年から1992年までの材料消費量のグラフである。若干ノイズは乗っているがデータはオーバーシュート＆振動を示している。

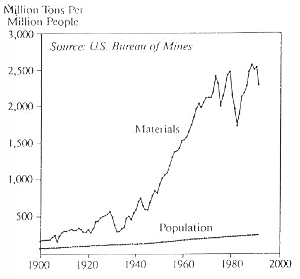
図８：合衆国における材料消費量の推移（1900 - 1992）

　図９は合衆国における1980年から1992年までの銀行・貯蓄貸付組合（savings and loan）・全金融機関の破綻の数の時間系列グラフである。これらは全てオーバーシュート＆崩壊を示している。

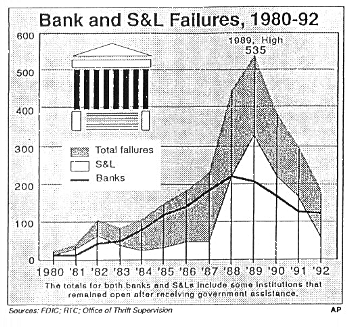
図９：合衆国における銀行・貯蓄貸付組合・破綻金融機関数の推移（1980 - 1992）

　図１０は日本における1950年から1994年までの穀物作付面積のグラフである。このデータの時間経路は逆Ｓ型を示している。

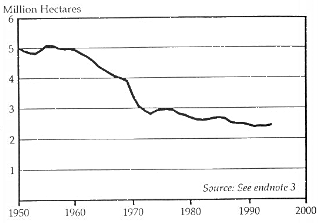
図１０：日本における穀物作付面積（1950 - 1994）

　これらのグラフから読者が読むとるべき一般的な結論は、現実のシステムが往々にして特徴的な時間系列を示し、これらのパターンを模倣してシステムダイナミクスモデルを構築することがでいるということである。

Updated : 2006/02/07