モンテカルロシミュレーションを行う。

設定内容

　メニューから［Poptools］→［Simulation tools］→［Integrate a system of ODEs］と選択すると以下のようなダイアログが表示される。

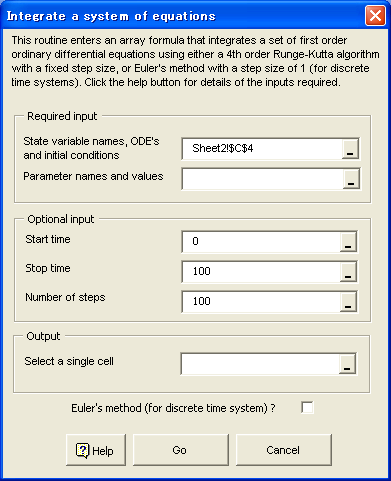
　このルーティンは連立常微分方程式を４次のルンゲ＝クッタアルゴリズムを用いて数値積分で解く。積分は全て PopTools DLL (RANDEVS.DLL) で計算され、Excel に渡される。with the results being returned to Excel as an array formula. Because the step size is not adaptive, the algorithm best suited to 努ell behaved・systems. The algorithm can be unstable if the system is stiff ・although you can often get around this by choosing a smaller step size, albeit at the expense of computational time. The output from the menu system is an array formula, ODEIntegrate, which takes the following arguments: Argument 1 is a contiguous Excel range containing three columns. The first column must be the names of the state variables, the second contains the ordinary differential equations written out as strings, the third contains the initial values of the state variables. For example, a host-parasite model could be specified as follows: X b*(X+Y+Z) - beta*X*Y - m*X 98 Y beta * X * Y - ( a+m+v ) * Y 2 Z v * Y - m * Z 0 Argument 2 is a contiguous Excel range containing two columns. The first column contains the names of the parameters, and the second is their values Argument 3 (optional) is the initial time. Default is time 0. Argument 4 (optional) is the finish time. Default is time 100. Argument 5 (optional) is the step size. Default is 1. The function returns a range of values with the integration variable 典・in the first column, and the values of the state variables in the remaining columns. You can define as many state variables and parameters as you like, but be prepared for slow performance on large problems. Each state variable must have a corresponding ODE and initial value, and all parameters must have a name and value. There is always an implicit variable with the label ("T" the integration variable), which you can include in any of the differential equations. (BE CAREFUL: You must not include a "T" in the list of state variable names passed to the function, because it is always included) There is no limit for the length of expressions that define the ODE痴. Spaces are ignored, and can therefore be used to make the expressions easier to read. Any combination of braces can be used, ie, ( ), { }, and [ ]. Braces must be in pairs, but need not be matched, since all are converted to ・・or ・・before being evaluated. Expressions are not case sensitive, hence 羨・is interpreted as the same variable as 疎・ Predefined variables: PI Accepted operators: + , - , * , / , ^ , MOD, DIV [ MOD and DIV implicitly perform a trunc() on their operands ] The following functions are supported; it doesn't matter if you use lower or upper case: COS, SIN, SINH, COSH, TAN, COTAN, ARCTAN, ARG, EXP, LN, LOG10, LOG2, LOGN, SQRT, SQR, POWER, INTPOWER, MIN, MAX, ABS, TRUNC, INT, CEIL, FLOOR, HEAV (heav(x) is =1 for x>0 and =0 for x<=0), SIGN (sign(x) is 1 for x>1, 0 for x=0, -1 for x<0), ZERO (zero(x) is 0 for x=0, 1 for x<>0), PH (ph(x) = x - 2*pi*round(x/2/pi)) RND (rnd(x) = int(x) * Random) RANDOM (random(X) = Random; the argument X is not used) Credits The ODEIntegrate function depends on a mathematical expression parser, which evaluates the string representation of each differential equation. The parser is quite fast ・apparently only 40-80% slower than similar compiled expressions ・although the evaluation of the ODEs in the DLL entails creation of expression parsers on the fly, and some pre-processing to check for errors. The parser was written in Object Pascal (Delphi) by: Renate Schaaf (1993) Alin Flaider (1996, 1997) Stefan Hoffmeister (1996, 1997) It is available on the web at the Delphi Super Page http://delphi.icm.edu.pl/ (search for TParser).

Update : 2005/04/21