回路解析だと、こういう風に、いきなり複素数の話が出てくる。まあ、使えば便利に記述できるからそれでもいいんだけど、もし何か意味があるならそれをきちんと説明してほしいのに、なかなかその説明に出くわさない。が、まあ、それに文句を言っても始まらないので、とりあえず本題。

　複素数は、実数と虚数を包含する数体系であって、実数 x,y と、虚数単位 j を用いて z = x + jy という形式で記述される。
　数学科出身の身ととしては非常に気持ち悪いのだが、まあ、虚数単位を i ではなく j で表すこと及び、虚数単位に乗じる係数を後ろに記述することはこの業界のしきたりらしいのでおとなしくそれに従うことにする。 i を使わないのは、電気の世界では何も言わずに i と言うと電流のことだということなんだろう。

複素数の表現方法

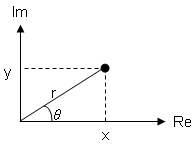
　複素数には様々な表現方法がある。

表示方法	表記
直交表示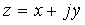
極表示（スタインメッツ表示）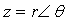
指数表示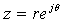
三角関数表示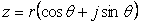

　これらの表現方法は等価なのだから、必要に応じて便利な表現で処理を行い、求められた表現に変換すればよい。

　複素数同士の和や差を求める場合、実際には実部・虚部のそれぞれの和または差を求めるわけだから、直交表示で行うのが最も簡単である。しかし乗算や除算の場合、直交表示ではまともに全項を計算する必要があるが、極表示や指数表示では、その名の通り指数演算を利用して計算を容易にできる。例えば

と計算できる。これを必要に応じて他の表示方法に変換すればよい。除算の場合は

となる。