前章でも書いたけれども、一般には回路に流れる電流はどんなものになるかは不明である。が、それではなかなか話がしにくい。んなわけで、たいていの回路解析では周期的に変動するものを扱う。その端的な例として三角関数を利用する。実関数が周期関数ならば（形式的には）フーリエ級数展開が可能であり、フツーの回路解析で扱うようなものでは、まあ、発散するようなのは考えないのでそのあたりを心配することはない。

インピーダンス

　１回路要素・回路における１つの枝路・回路全体において、それに流れる電流とそこにかかる電圧の比をインピーダンスと言う。要するに、抵抗・リアクタンス（の微分みたいなもの）・キャパシタンス（の逆数みたいなもの）を統合的に説明する名前というか概念がほしかったわけで。

Updated : 2006/12/18

位相角度

　上記のインピーダンスは、回路要素が抵抗の場合はスカラーと見なせるが、回路要素がコイルやキャパシタの場合、インピーダンスはスカラーと見なせない。
　電圧と電流がともに三角関数（以下では正弦波であることにしよう）であれば、抵抗でなければ角度（位相）にズレが生じる。このズレを位相角度と言う。

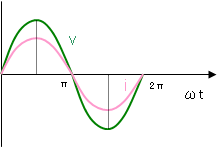
　抵抗の場合は、電流と電圧は同位相であり、インピーダンスの大きさは R である。

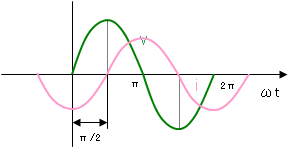
　インダクタンスの場合は、電流は電圧よりもπ／２だけ遅れる。インピーダンスの大きさは ωL である。

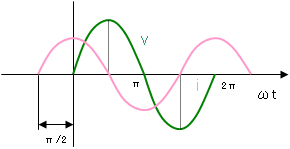
　キャパシタンスの場合は、電流は電圧よりもπ／２だけ進む。インピーダンスの大きさは 1/ωC である。

Updated : 2006/12/18

直列と並列

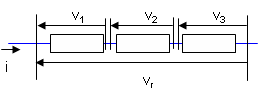
　直列回路では、各回路要素にかかる電圧の総和が回路全体の電圧に一致する。
　v_r = v₁ + v₂ + v₃

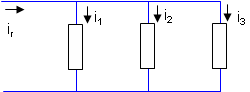
　交流回路では、各枝路を流れる電流の総和が回路全体を流れる電流に一致する。
　i_r = i₁ + i₂ + i₃

Updated : 2006/12/18