Title : Tactics

|
Location : Home > Methods > Simulation > Multi Agent System Title : Tactics |
 |
エージェントの行動選択の原理について
前章においては、エージェントの特質として「環境の知覚」「行動の選択」「環境への影響」を挙げたが、研究事例を見ると、「行動の選択」に関するものが多く見られる。そこでここでも行動の選択に関する方法を取り上げ、まとめることとする。
1.ゲーム理論
「エージェントは環境を知覚し、行動を決定する」と言った時の「環境」には他のエージェントの行動(による結果)も含まれる。基本的には各エージェントは独立に自分の目標達成のための行動を採るが、同一の目標に向かう他のエージェントと協調して問題解決を早めるか、競合相手とみなして排除するかによって具体的に採るべき行動が変化するし、またその影響によって環境も変化する。(その相乗作用で当初は想定もしなかった集団行動が発生することがあるのでマルチエージェントは面白い。)
ゲームの基本型
ゲーム理論(Game Theory)は J. von Neumann と O. Morgenstein によって著された『ゲームの理論と経済行動』が出発点となっている。
ゲームは
【ひとりごと #01】
そのような指標が存在するのか否かという議論は可能だが、それは経済学における効用関数の存在の是非をめぐる議論で済んでいることにしてるのだろう。
そして各プレイヤーは(基本的には)自分の利得関数を最大化するように行動する。
自らの利得関数を最大化させるなど、プレイヤーが論理的に一貫性のある行動を選択する場合、合理的(rational)であるという。
【ひとりごと #02】
「基本的には」というただし書きをつけたのは、各プレイヤーにエージェント全体の利得関数を最大化するように行動を選択させるという、「利他的」な性質を持たせることも可能であるので、必ずしも「各プレイヤーは自分の利得関数を最大化するように行動する」とは言えないため。
ゲームGを次のように定式化する。
G=<I,A,U>
I={1,2,…,n}:プレイヤーの集合
A={A1,A2,…,An};Ai:プレイヤー i の採りうる行動の集合
U={U1,U2,…,Un};Ui:プレイヤー i の利得関数
特に、プレイヤーが2人で行動集合が有限である場合は利得関数を行列の形に表示することができて、以下のようになる。
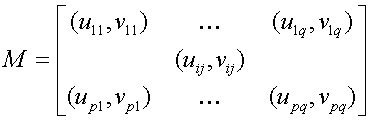
すなわち、プレイヤー1の行動が i で、プレイヤー2の行動が j である場合のそれぞれの利得関数がuij、vijであることを示している。
ゲームの種類
各プレイヤー間のコミュニケーションの可否や、拘束力のある合意の形成の可否によってゲームの様相が異なる。各プレイヤーがそれぞれ個別に自身の目的の達成のために行動を選択するゲームを非協力ゲーム(non-cooperative game)と言う。一方、プレイヤー間のコミュニケーションが可能で、合意形成可能なゲームを協力ゲーム(cooperative game)と言う。
ゲームの反復の有無などによっても様相が異なる。
ただ一度の行動選択を扱うゲームをゲームを戦略型ゲーム(game in strategic form)と言う。おそらくゲーム理論の提唱が必要とされた、戦場における戦術(または戦略)選択の場面において、彼我の採りうる手段と目的を分析しただ一度の選択で最大の効果をもたらすために考えられたからこのような名称がついているのであろう。
また、プレイヤーの採った行動を木構造で表現した(表現しうる)ゲームをゲームを展開型ゲーム(game in extensive form)と言う。チェスや将棋の棋譜の記録はこの部類に入るだろう。また戦略型ゲームの複数回繰り返しで表現されるゲームを繰り返しゲーム(iterated game)と言う。
また、上段の2人によるゲームの例で、 p = q かつ uij = vjiであるとき、ゲームは対称的(synmetric)であると言い、すべての i,j について uij + vij = C (定数)であれば定和ゲーム(constant-sum game)と言う。特にC = 0 の場合をゼロ和ゲーム(zero-sum game)と言い、それ以外を非ゼロ和ゲーム(non zero-sum game)と言う。
…以下、ゲーム理論についてはいろいろ書くことはあるんだが、それは別途ゲーム理論のページを作ったときに詳しく触れることにして。
2.学習理論
エージェントの振る舞いを考える場合、環境によってその行動が一意に定まれば定式化は可能であるのだが、現実の社会や自然界においては、エージェントが環境により順応したり、他のエージェントの振る舞いを見て、さらに「賢く」なることが考えられる。この状況を実現するのに、人工知能の分野で用いられる学習理論を用いることが多い。
ニューロンモデル
人間の脳における神経細胞の情報処理メカニズムを McCulloch と Pitts が模擬的に定式化したモデルを形式ニューロンといい、ニューラルネットによる学習の基礎になっている。
MacCulloch & Pitts モデルは多入力1出力のシステムと考えることができる。
![]()
すなわち、0または1の入力を採る各入力要素xi(i=1,2,…,n)に対し重みωiつきの加重値がある閾値θを超えれば出力信号 y に1が出力され、そうでないときは0となるようなシステムである。ただしここで関数S(*)はヘビサイド関数と呼ばれる、
![]()
で記述される関数である。
パーセプトロンモデル
Rosenblatt はニューロンを構成要素とし、感覚層(S層)・連合層(A層)・反応層(R層)の3つの層を持つモデルを提案した。
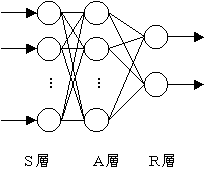
これを(単純)パーセプトロンと言う。層がいくつあっても結果的には最後の出力部分への入力とその重みが意味を持つので、実質的に2層のニューラルネットワークと同等である。
y = Σωixi - θを n次元空間における(n-1)次元の超平面Pと考えれば、点(x1,x2,…,xn,y)の集合のうち、y=1である点の集合とy=0である点の集合が、それぞれ超平面Pの一方にあるようにすることができる場合がある。このとき、この関数は線形分離可能(linearly separable)であると言う。
結果 y が与えられた時に、線形分離可能となるように重みωiと閾値θを探索することができれば、より正確な行動選択ができるようになる。この性質を利用して学習をさせることができる。具体的な学習方法については、例えば「多層パーセプトロン」、「パーセプトロンの学習」などを参照のこと。
誤差逆伝播学習(バックプロパゲーション)
ニューラルネットによる学習でよく用いられているのが、Rumelhartらによって提唱された誤差逆伝播学習(back propagation)である。これは入力の列に対して望ましい結果信号(教師信号)が提示され、それにしたがって重みを調整していく方法であるので、教師あり学習(supervised learning)とも言われる。この場合、誤差関数(Error function)を計算し、その極小化を目指すように重みを調整していく。通常、誤差関数は、出力値と教師信号の差の平方和(の定数倍)が用いられる。
強化学習
しかし実際のさまざまな局面では、教師信号が得られるとは限らない。その場合でも行動を選択し、その結果の望ましさに応じて学習していかねばならない場合がある。このような学習を教師なし学習(unsupervised learning)と言う。その1手法として強化学習(reinforcement learning)がある。
具体的には、例えば「強化学習システムの設計指針」、「強化学習」「強化学習FAQ」などを参照のこと。
最近は強化学習の中でも、TD学習(Temporal Difference Learning)と呼ばれる手法が主流になりつつある。これは、現在の評価値とその次の行動の結果得られた評価値(を現在価値に割り引いた価値)の差をもとに評価値を更新していく手法である。
詳しくは、例えば
さらに、Q学習(Q-Learning)と呼ばれる手法がある。単純なTD学習では、いわば行き当たりばったりで採った行動の結果がどうであったかということから学習するという面がぬぐえない。本来目指すべきは、最も望ましい行動の選択のはずである。
そこで、ある状態で採った行動が最適になるような指標を導入し、その推定値が向上するように逐次更新していく手法が提唱されている。これがQ学習である。
詳しくは、例えば
3.進化型計算
進化型計算(evolutionary computation)も、広義の学習理論と言えるのかも知れない。ただし各エージェントが個別に学習するというよりは、集団として「よい」ものを残していくという傾向がある。この分野で最も有名なモデル(というより計算法)は J. Holland の提唱した遺伝的アルゴリズム(GA ; Genetic Algorithm)である。
遺伝的アルゴリズム
遺伝的アルゴリズムは、各エージェントを個別の生物のようにみなし、各エージェントに遺伝子(gene)を与え、生物学的遺伝と同様に交差(crossover)・突然変異(mutation)・選択(淘汰)(selection)を通じて、より適合度(fitness)の高い遺伝子を残すことで、より環境(と与えられた問題)に適した遺伝子を多く残すことを目指すものである。
参考文献
 |
Updated : 2002/11/11 |