交流回路の場合、電圧と電流との関係が必ずしも比例関係にない。これによりある時刻の電流×電圧の値が、直流の場合に想定できる電力の量にならない。１Ａで１０Ｖかけているのに１０Ｗにならなくて、９Ｗとかになったらそれはそれで無駄になっているような気がする。そこでその「無駄」の割合をできるだけ減らすことを考えるものらしい。

力率

　ある回路に電圧 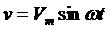が加えられたとき、電流 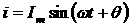が流れるものとする。このとき電力は以下の式で表される。

　この式は、瞬時電力 p が定数項と、（平均値が０である）正弦波項からなることを示していることから、瞬時電力 p の平均 P は以下のように表される。

　すなわち　［電力の平均値］＝［電圧実効値］×［電流実効値］×［ある比率］　という形式になっている。この［ある比率］（cosθ）のことを力率（Power factor）と言う。p.f. とも表す。電流が電圧よりも遅れている誘導性回路（inductive circuit）では遅れ力率（lagging power factor）を持ち、電流が電圧よりも進んでいる容量性回路（capacitiveinductive circuit）では進み力率（leading power factor）を持つ。
　平均電力 P は有効電力と呼ばれ、Wで表す。
　これに対し積 VI を皮相電力（apparent power）と言い、記号 S で表し、単位はVA である。
　これに対し積 VIsinθ を無効電力（reactive power）と言い、記号 Q で表し、単位はvar (volt ampere reactive) である。

複素電力

　有効電力・皮相電力・無効電力の関係はベクトルで表記することができる。これを電力ベクトル図（power triangle）と言う。

すなわち
　［有効電力］＝［電力］×［電流の同相成分］
　［皮相電力］＝［電力］×［電流］
　［無効電力］＝［電力］×［電流の直角成分］
と考えることができる。

　これを複素平面で考えたとき、複素電力（complex power）と言う。皮相電力 S を複素数とみなすと有効電力 P はその実部、無効電力 Q はその虚部とみなすことができる。

　電流を V = Ve^jα、電流を I = Ie^{j（α＋θ）} としたとき、複素電力 S は以下のように表せる。

力率改善

　通常、電力は負荷が単位時間に消費する仕事量で計測される。この電力はトランスにより供給されるが、その定格は kVA で表されている。もし力率が小さいと実際に負荷で消費する電力に対し、トランスで供給しなければならない電力（皮相電力）が大きくなる。逆に力率が大きいと効率的に電力を消費することになる。回路の構成要素を変えず、接続方法などを変えることで力率を変更して効率的にすることを、力率改善と言う。